圧縮センシング-基礎1

[O-2-228] 高次の静磁場不均一性を考慮したSelf-Calibrated Compressed Sensingアルゴリズムの開発

^〇玉田大輝, 巨瀬勝美 (筑波大学大学院数理物質科学研究科　電子・物理工学専攻)

【背景】圧縮センシング(CS)は，静磁場の不均一性がある場合，k-spaceにエラーが引き起こされ，正しく再構成することが困難である．そこで，本研究では，Cross-Sampling法(CrSa)とTime-Segmented法(TS)を用いることによって，高次の静磁場不均一性の下でCSを行う手法を提案する．
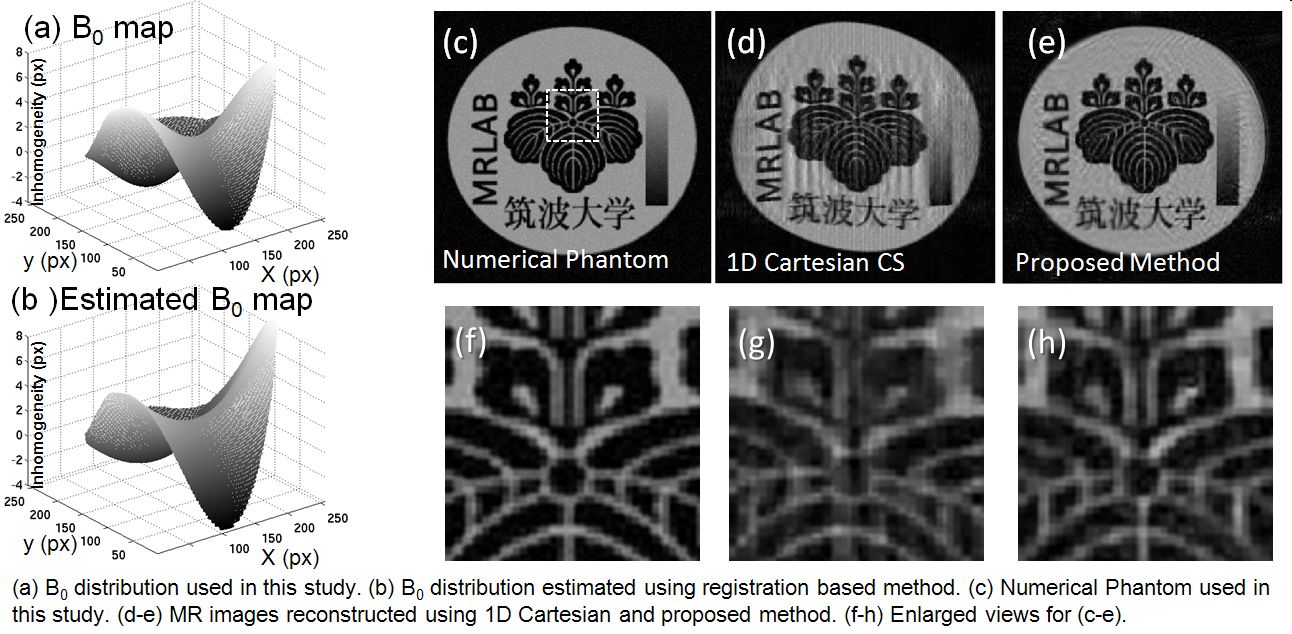
【方法】信号のアンダーサンプリングには，CrSaを用いた．静磁場分布はregistrationベースの手法を用いて推測した．MR画像は，L1ノルム最小化法を用いて再構成した．また，不均一性によるk-spaceの歪み補正は，TSを用いて行った．　本手法の有用性を確認するため，数値ファントムを用いた再構成シミュレーションを行った．静磁場不均一性については，図(a)で示すような分布を想定した．静磁場不均一性によるT2*の効果については無視した．
【結果・考察】画像(b)は，本手法で推測した磁場分布である．与えた磁場分布とのエラーはRMS値で0.38 pixであった．画像(c)は今回用いた数値ファントムである．また，画像(d, e)は，それぞれ従来手法（1D Cartesian法, R=2.5），本手法(R=2.5)を用いて再構成した画像である．また，画像(f-g)は，これらの拡大画像である．従来手法に比べ，本手法による再構成画像には歪みやアーチファクトが少ないことがわかった．
【結論】CrSaとTSを用いて非線形な静磁場不均一分布の下でSelf-CalibratedのCSを行うことに成功した．今後は実際のMRIスキャナーへの実装を目指す．